Снабжение потребителей торговой организацией: взгляд через призму экономико-математического моделирования

 В статье рассмотрена экономико-математическая модель снижения издержек управления текущими многономенклатурными товарными запасами в торговой ор-ганизации с учетом ограниченности площадей ее складских помещений. Модель основана на простейшем уравнении Уилсона, построенном на следующих основополагающих предположениях: на склад организации товары завозятся мгновенно с окончанием их запасов; продолжительность времени между следующими друг за другом поставками товаров за определенный период (год) одинакова; годовая потребность на товары устанавливается вне модели.

Несмотря на то, что модель идеализирована, она обладает практической ценностью. Придерживаясь описанной в ней схемы, организация может контролировать эффективность процесса управления текущими товарными запасами путем сопоставления фактически сложившихся издержек с определяемыми с помощью модели издержками. Предлагаемая читателю методика реализована на примере малой торговой фирмы ООО «Сатурн».

1. Построение оптимизационной модели снабжения товарами потребителей торговой организацией

Постановка экономической задачи

ООО «Сатурн», занимающееся торгово-закупочной деятельностью, осуществляет операции по завозу товаров либо на собственный, либо на арендованный склад. Созданные текущие товарные запасы подлежат дальнейшей продаже потребителям на основе заключенных с ними контрактов. Операции ввоза товаров и их размещения в складских помещениях, а в дальнейшем доставка потребителям, связаны с определенными издержками. Прежде всего это издержки по формированию текущих товарных запасов. Эффективная система снабжения предполагает определение таких размеров запасов, которые отвлекают наименьшие средства на оформление заказов, транспортировку, хранение и содержание на складе. Затраты на оформление заказов с поставщиками товаров для торговой фирмы включают: затраты на телефонную связь, телеграф, представительские расходы, командировочные расходы и др. Затраты на транспорт по ввозу товаров на собственный склад вместе с затратами на оформление заказов позволяют определить накладные расходы в расчете на одну партию завоза товаров. Совокупные накладные расходы, затраты хранения и содержания товарных запасов на складе формируют издержки управления текущими товарными запасами. В таких условиях фирма заинтересована в создании рациональных размеров запасов, минимизирующих издержки управления. Между тем если не принимать во внимание то обстоятельство, что площади складского помещения ограничены для размещения запасов, то фирме придется нести лишние, неоправданные расходы на аренду дополнительных площадей. Построение математической модели сформулированной задачи требует введения обозначений.

Обозначения

ООО «Сатурн» приобретает и реализует потребителям в течение предстоящего хозяйственного года несколько номенклатурных групп товарных позиций. В дальнейшем анализе будем иметь в виду номенклатурную группу товаров «Бакалея», содержащую достаточно широкий ассортиментный перечень. Для построения математической модели управления запасами номенклатурной группы бакалейных товаров с целью их завоза на собственный склад и дальнейшей продажи потребителям необходимо определить объемы завоза каждого вида товара, накладные расходы на оформление и транспортировку одной партии поставки, затраты на хранение и содержание единицы товара в запасе.

В общем случае будем считать, что количество ассортиментных позиций бакалейных товаров составляет n ().

Q_i — годовой объема завоза i-го вида бакалейной продукции.

C_i — накладные расходы на оформление заказов и транспортировку одной партии поставки i-го вида товара.

K_i — затраты хранения и содержания на складе единицы i-го вида бакалейного товара в запасе.

s_i — складская площадь, отводимая для хранения единицы i-го вида товарного запаса.

S — общая складская площадь.

x_i — переменная, характеризующая количество запасов i-го вида товара в одной партии завоза на склад.

F(X) — функция n переменных, показывающая общие издержки управления запасами n видов товаров, а X = (x₁, x₂, …, x_n) — объемы запасов каждого вида товара в одной партии поставки.

Построение математической модели

Суммарная величина издержек управления текущими товарными запасами в введенных обозначениях составит:

Общая складская площадь, занимаемая товарными запасами всех видов в искомых их количествах, будет равна ,

а ограничение по общей складской площади примет вид:

Математическая модель управления текущими товарными запасами заключается в определении такого вектора X = (x₁, x₂, … x_n), при котором значение функции издержек управления (F(X)) становится минимальным, а при таких размерах запасов занимаемая ими складская площадь не может быть больше фактической ее величины.

 (*)

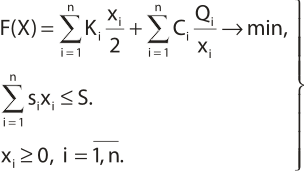Полученная математическая модель (*) представляет собой задачу нелинейного программирования, которую можно решить на основе фактических значений параметров с применением современных программных продуктов (например, Mathcad, Maple и др.). Мы остановимся на классической схеме ее решения, заключающейся в применении функции Лагранжа (без учета условий неотрицательности переменных), одновременно проводя расчеты с помощью программного продукта Maple. Это можно объяснить необходимостью определения численного значения нового параметра , который имеет весьма информативное экономическое содержание. Функция Лагранжа выглядит так:

В точке минимума значения функции Лагранжа и функции издержек управления запасами численно равны. Поэтому применяя метод определения частных производных функции  L(x₁, x₂, …, x_n, )    по переменным  x₁  () и  получим систему из (n + 1) алгебраических уравнений с (n + 1) переменными.

 (**)

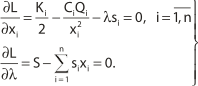Выражая переменные x_i для каждого i с помощью неизвестного параметра , получим:

Подстановкой последнего выражения для x_i в (n + 1)-е уравнение системы (**)? приходим к иррациональному уравнению для определения параметра :

Определив значение  = *, можно установить оптимальный размер запасов каждого вида товара в одной партии завоза на склад торговой организации (x_i*):

С помощью последней формулы можно определить оптимальные значения ряда показателей управления запасами и снабжения торговой фирмы:

1) оптимальную частоту завоза одной партии i-го вида продукции:

2) оптимальную продолжительность времени в днях между двумя соседними завозами запасов i-го вида товара:

3) минимальную величину издержек управления многономенклатурными запасами товаров:

min F(X) = F(X*).

Применение построенной выше математической модели в практической работе ООО «Сатурн» позволит определить условия и последовательность его снабжения с учетом ограниченности общей складской площади, устанавливая при этом оптимальные значения ряда параметров эффективности функционирования торговой фирмы.

2. Экономико-математическая модель  управления текущими товарными запасами

 ООО «Сатурн» в своей торгово-закупочной деятельности собственным складским помещением пользуется только по ограниченной номенклатурной группе товаров «Бакалея». Площади дефицитны, для размещения других товарных позиций фирма их арендует, поэтому есть необходимость строительства складского помещения.

Сложившаяся динамика работы исследуемой фирмы с потребителями и поставщиками бакалейных товаров показывает, что годовые объемы поставок части бакалейной продукции стабилизировались на фиксированном уровне. Поэтому размеры поставок товаров на 2009 г. поддаются определению. Наиболее востребованными продуктами питания являются крупы, сахар, сгущенное молоко, мясные консервы. Эти виды бакалейных товаров закупаются предприятием в упаковочных ящиках, вмещающих определенное количество фасованных по 1 кг крупы и сахара, а также сгущенного молока и мясных консервов в металлических баночках. Завоз товаров на склад фирмы и их размещение осуществляется в упаковочных ящиках. В дальнейшем за единицу товара будем принимать одну упаковку каждого вида бакалейной продукции. На основе сложившейся практики соблюдения условий контрактов ООО «Сатурн» с поставщиками перечисленных товаров автором статьи установлены средние накладные расходы одной партии завоза для каждого товара, а также рассчитаны затраты хранения и содержания в складском помещении в расчете на единицу (упаковку). Площадь, занимаемая одним упаковочным ящиком по каждому виду продукта, легко поддается расчету. Общая величина площади склада известна.

Исходные данные по всем перечисленным бакалейным товарам приведены в табл. 1, на основе которой проводится оптимизация количества упаковочных ящиков по каждому виду продукта в одной партии завоза на склад. В табл. 1 использованы введенные в предыдущем подразделе статьи обозначения.

Общая площадь складского помещения составляет 670 м².

Таблица 1. Основные характеристики завоза бакалейных товаров  на склад ООО «Сатурн» в 2009 г.

Для определения оптимального количества упаковок в одной партии поставки по каждому виду продукта питания воспользуемся формулами, полученными на основе математической модели (*), прежде всего, для расчета оптимальных величин следующих переменных:

x₁ — количество упаковочных ящиков, содержащих крупу в одной партии завоза;

x₂ — количество упаковочных ящиков, содержащих сахар в одной партии завоза;

x₃ — количество упаковочных ящиков, содержащих металлические баночки сгущенного молока;

x₄ — количество упаковочных ящиков, содержащих металлические баночки мясных консервов.

3. Определение оптимального количества запасов товаров в одной партии завоза

Иррациональное уравнение, необходимое для получения значения параметра , приобрело вид:

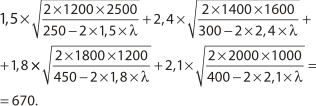
В результате решения этого уравнения получено:  ≈ –71,65. Исходя из этого можно определить средние текущие запасы каждой анализируемой позиции бакалейной продукции. В частности мы получим следующие результаты:

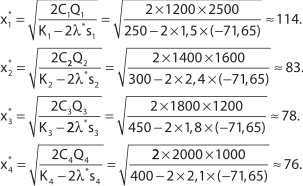
На основе полученных оптимальных значений количества упаковочных ящиков по каждой позиции бакалейных товаров целесообразно определить среднюю частоту их завоза на склад ООО «Сатурн».

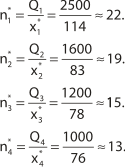
Также можно рассчитать среднюю продолжительность времени между двумя соседними завозами каждой бакалейной позиции в днях в течение предстоящего года.

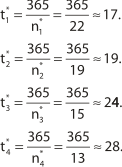
Минимальная (оптимальная) величина издержек управления текущими запасами перечисленных видов бакалейных товаров с учетом ограниченности полезной площади складского помещения составит (руб.):

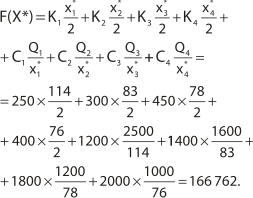
Таким образом, минимальная величина издержек, связанных с организацией завоза бакалейных товаров на склад предприятия, на 2009 г. составит 166 762 руб.

Параметр  с математической точки зрения представляет собой неопределенный множитель Лагранжа. Однако он имеет вполне определенный экономический смысл: если его значение отрицательно, то это говорит о том, что ООО «Сатурн» катастрофически не хватает собственных складских площадей. Фирма в среднем ежеквартально теряет 71,65 руб. с одного квадратного метра дефицитной для нее складской площади.

Издержки управления текущими запасами рассматриваемых видов продовольствия в 2008 г. составили 350 000 руб., а на 2009 г. фирма запланировала их на уровне 450 000 руб., что превышает оптимальный уровень на 283 238 руб.

Все полученные результаты сведены в табл. 2, в которой отражен также размер экономии на затратах при использовании предлагаемой нами методики оптимизации издержек управления запасами.

Таблица 2. Оптимизация снабжения ООО «Сатурн» по ассортиментной группе бакалейных товаров

Таким образом, оптимизация снабжения ООО «Сатурн» по выделенной группе бакалейных товаров позволяет существенно снизить издержки управления текущими запасами по сравнению с плановой их величиной и привести к экономии затрат в размере 283 238 руб.